
Произведение « Способ образования сферических и других поверхностей при помощи цилиндрических поверхностей» созданное автором по имени Васильев Валерий (Vasilev Valeriy valeryv@rambler.ru), публикуется на условиях лицензии Creative Commons «Attribution-NonCommercial-ShareAlike» («Атрибуция — Некоммерческое использование — На тех же условиях») 4.0 Всемирная.
Васильев В.А. Способ образования сферических и других поверхностей при помощи цилиндрических поверхностей.
Формулировка задачи.
В строительстве куполов принята следующая классификация типов купольных структур:
(а) Ребристый купол, (b) Усечённый ребристый купол, (c) Купол Шведлера, (d) Усечённый купол Шведлера,
(e) Ламельный купол, (f) Усечённый ламельный купол, (g) Диаматический купол, (h) Диаматический купол,
(i) Купол трёх-лучевой сетки, (j) Купол четырёх-лучевой сетки, (k) Геодезический купол, (l) Геодезический купол.
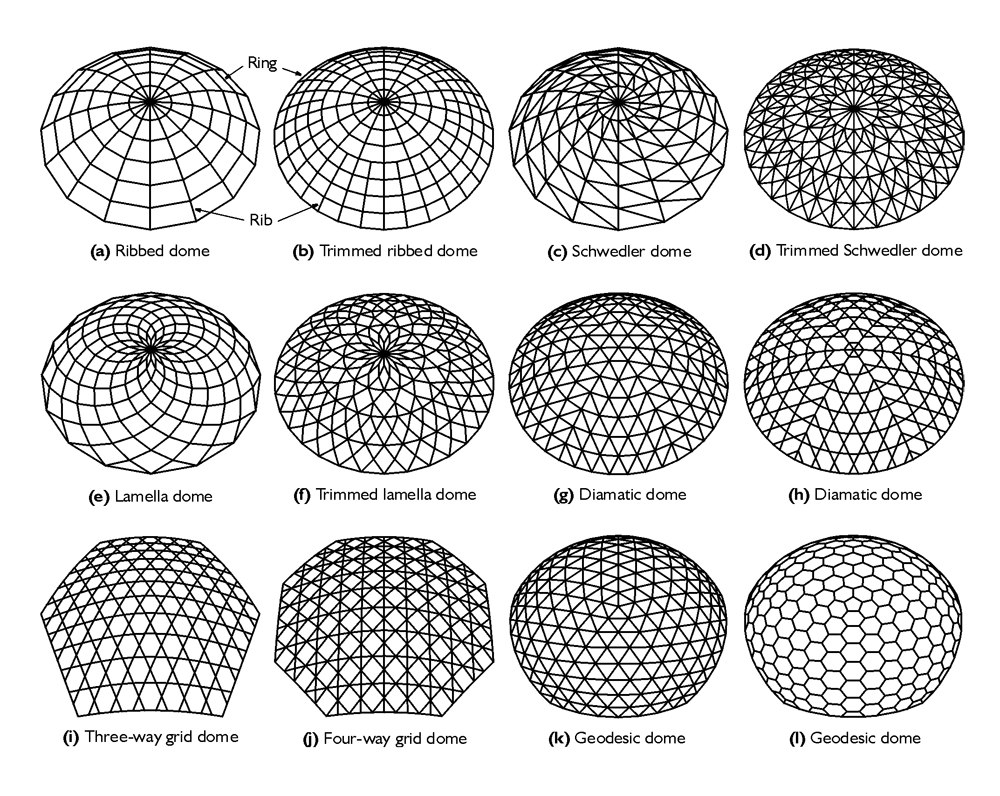
Рис.1 Классификация типов купольных структур
Основанием для такой типизации является конструктив купола, выполненный из линейных элементов. При этом вопрос покрытия купольных структур отходит на второй план.
Если же посмотреть на купол с точки зрения покрытия, то можно увидеть, что сферическая поверхность в этих куполах покрыта элементарными ячейками, которые являются различного рода многогранниками: трапециями, треугольниками, дельтоидами, ромбами, пяти и шестиугольниками.
Листовой же материал выпускается в виде квадратных или прямоугольных листов или полос.
Покрытие всех вышеприведённых типов купольных структур сопряжено с большим количеством разрезаний и дополнительных соединений и/или перерасхода листовых материалов. Зачастую вырезаемые многоугольники довольно сложны в построении.
Как уменьшить количество резов при покрытии купольной структуры с использованием стандартных листовых материалов?
Решение задачи.
При использовании листовых материалов удобно если большáя часть элементарных ячеек представляет собой квадраты или прямоугольники (прямоугольные полосы).
Нижеприведённый способ разбивки я изобрёл, глядя на стратодезические, ребристые купола. В этих куполах образующие их круговые/эллиптические дуги могут быть именно дугами, а не ломаными линиями. Визуально они выглядят как сферы, а не как многогранники.
Меридианная дуга в стратодезическом куполе является направляющей для цилиндрической поверхности, но эти поверхности имеют разную ширину от начальной внизу до нулевой в зените, являясь сферическими треугольниками. А если не уменьшать ширину? Тогда цилиндрическую поверхность легко укрыть полосой, изогнув её по рёбрам.
В отличие от стратодезических куполов, рёбра которых расположены по меридианам, в предлагаемом мной способе рёбра располагаются парами параллельно меридианам на одинаковом от меридиан удалении a/2, рис.2. Параллельные рёбра образуют цилиндрические поверхности, которые можно укрыть полосой шириной a.
Следующий шаг: перекрещиваем две таких поверхности под прямым углом через зенитную точку. Получилось следующее: каждая параллельная пара 90°-х (от опор до верхних точек) начальных опорных дуг образует и ограничивает цилиндрическую поверхность. Осталось правильно расположить эти направляющие на сферической поверхности, рис.2 .
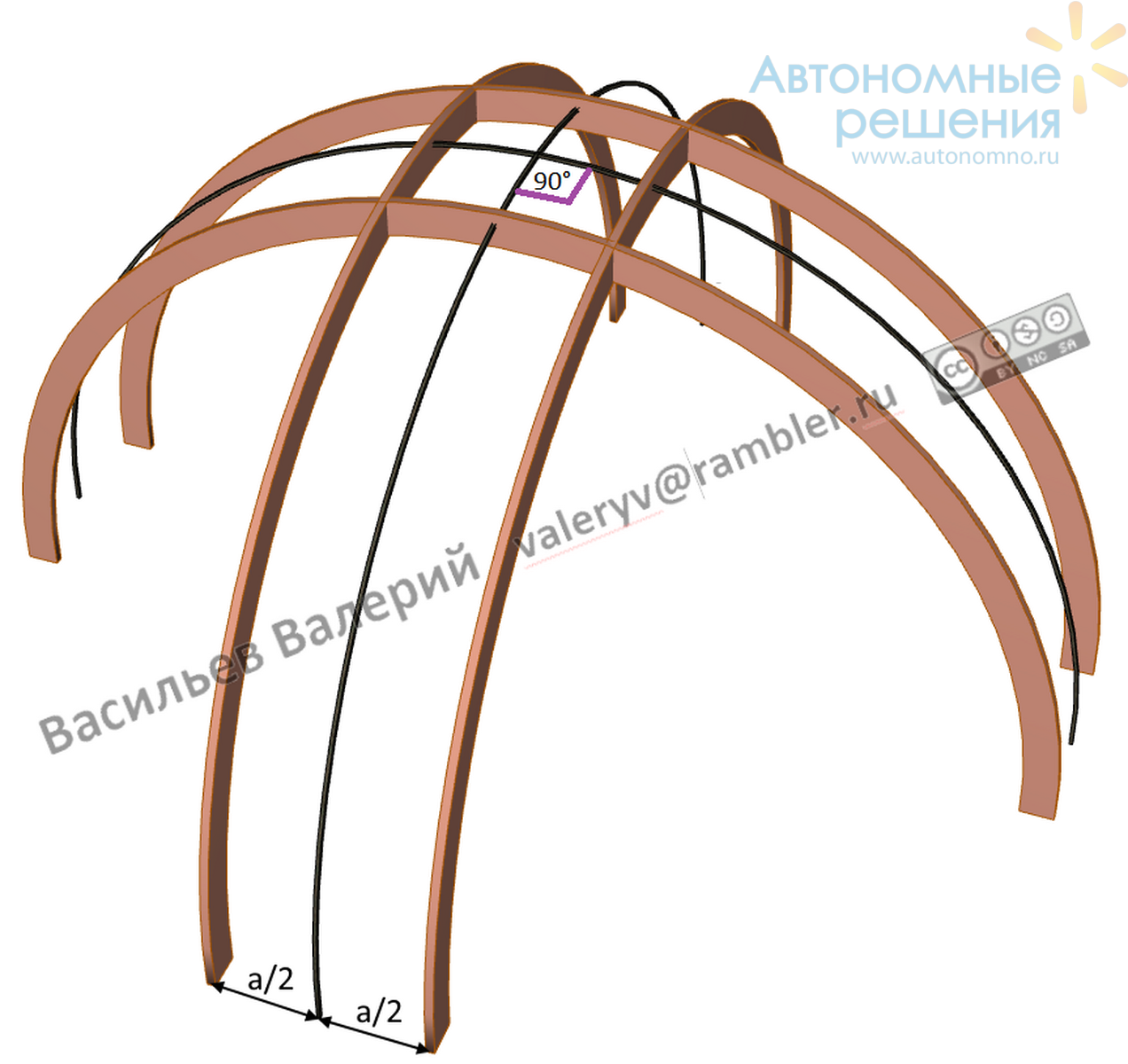
Рис.2 Расположение четырёх пар 90°-х начальных опорных дуг
Следует отметить, что похожий элемент можно увидеть на сайте компании SIPsmart Building Systems http://www.sipsmart.com, которая занимается дизайном и проектированием куполов на основе геодезического триаконтаэдра (Geodesic Triacontahedron) как модификации ромбического триаконтаэдра, рис.3.
В этом случае оранжевые секции вставлены как дополнение, которое позволяет раздвинуть геодезический триаконтаэдр. (Аналогичное решение в одном направлении используется и в надувных ангарах.)
Однако в этом случае это лишь «дополнительные» вставки для базовой фигуры.
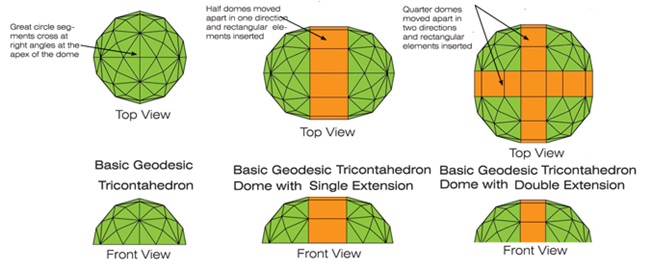
Рис.3 Геодезический триаконтаэдр
Далее поворачиваем копии начальных направляющих на угол равный 1/2 угла (в показанном случае это 45°) между соседними парами направляющих, вокруг зенитной вертикали (оси нормальной к опорной поверхности и проходящей через наивысшую, зенитную точку купола) рис.4.
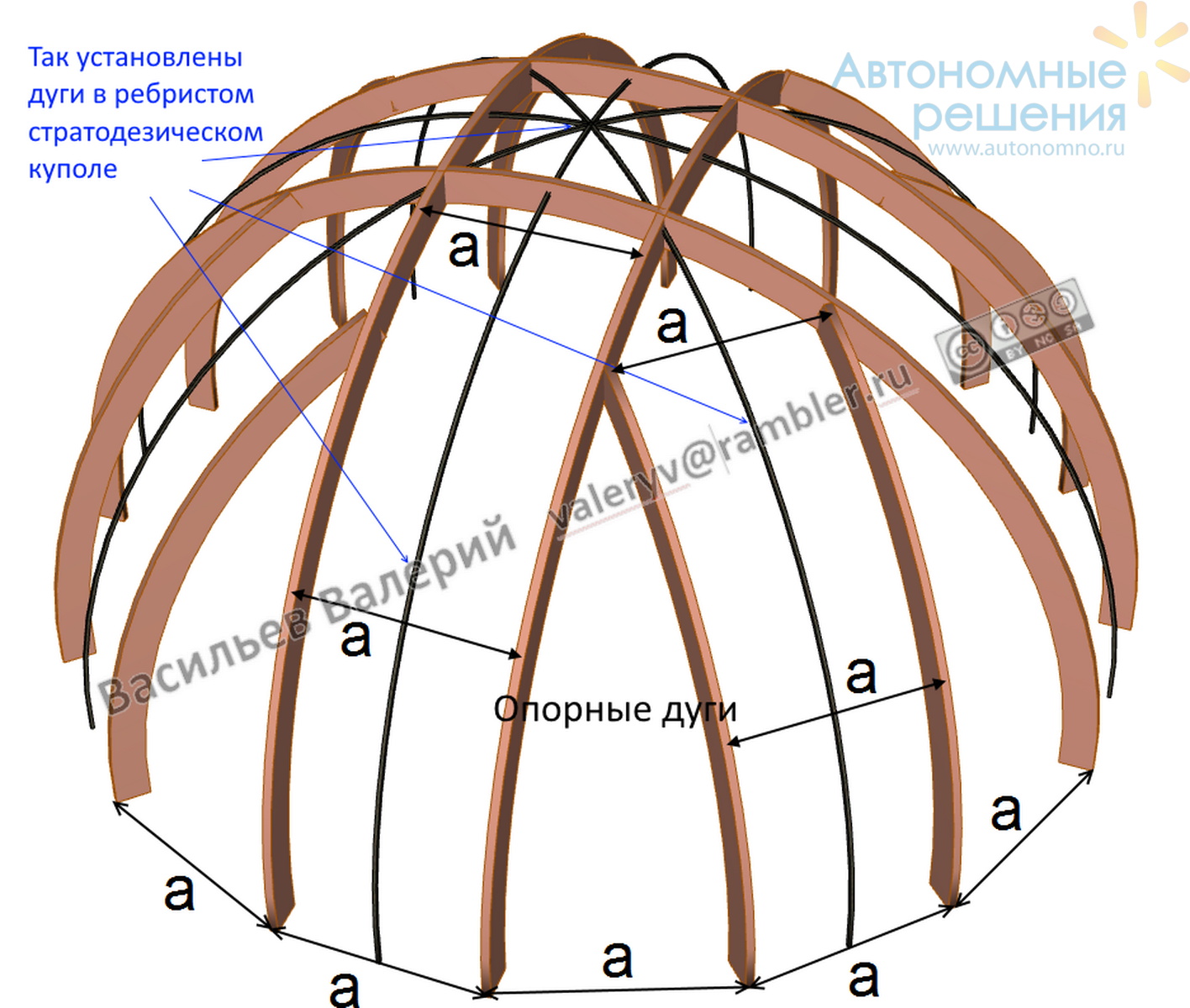
Рис.4 Восемь пар опорных дуг с одинаковым расстоянием между ними на опорной плоскости
Желательно иметь расстояния между опорными дугами на опорной плоскости равными (a) или не сильно отличающимися, это позволит использовать листовой материал без лишних сращиваний и разрезов. Если размер "a" равен ширине листового материала (1200, 1250, 1500, 1525 мм), то количество резов листов в поверхностях, между направляющих дуг будет минимальным и предельно простым (отрезание лишних полосок параллельно ширине). При этом на опорной плоскости образуется правильный многоугольник (16-ти угольник в приведённом варианте), рис.5.
В любых местах можно расположить укрепления в виде укосов между опорных дуг, пример на рис. 11д.
Поверхности между парами начальных (первичных) опорных дуг полностью укрываются полосами или прямоугольными листами, подрезка боковых сторон листов не требуется.
Поверхности между парами вторичных, третичных и т.д. опорных дуг до мест окончания этих дуг также укрываются полосами или прямоугольными листами, а выше остаются сравнительно небольшие треугольники.
Поверхности между соседними непарными опорными дугами являются сферическими треугольниками, аппроксимируются и укрываются листами, которые необходимо подрезать с боков.
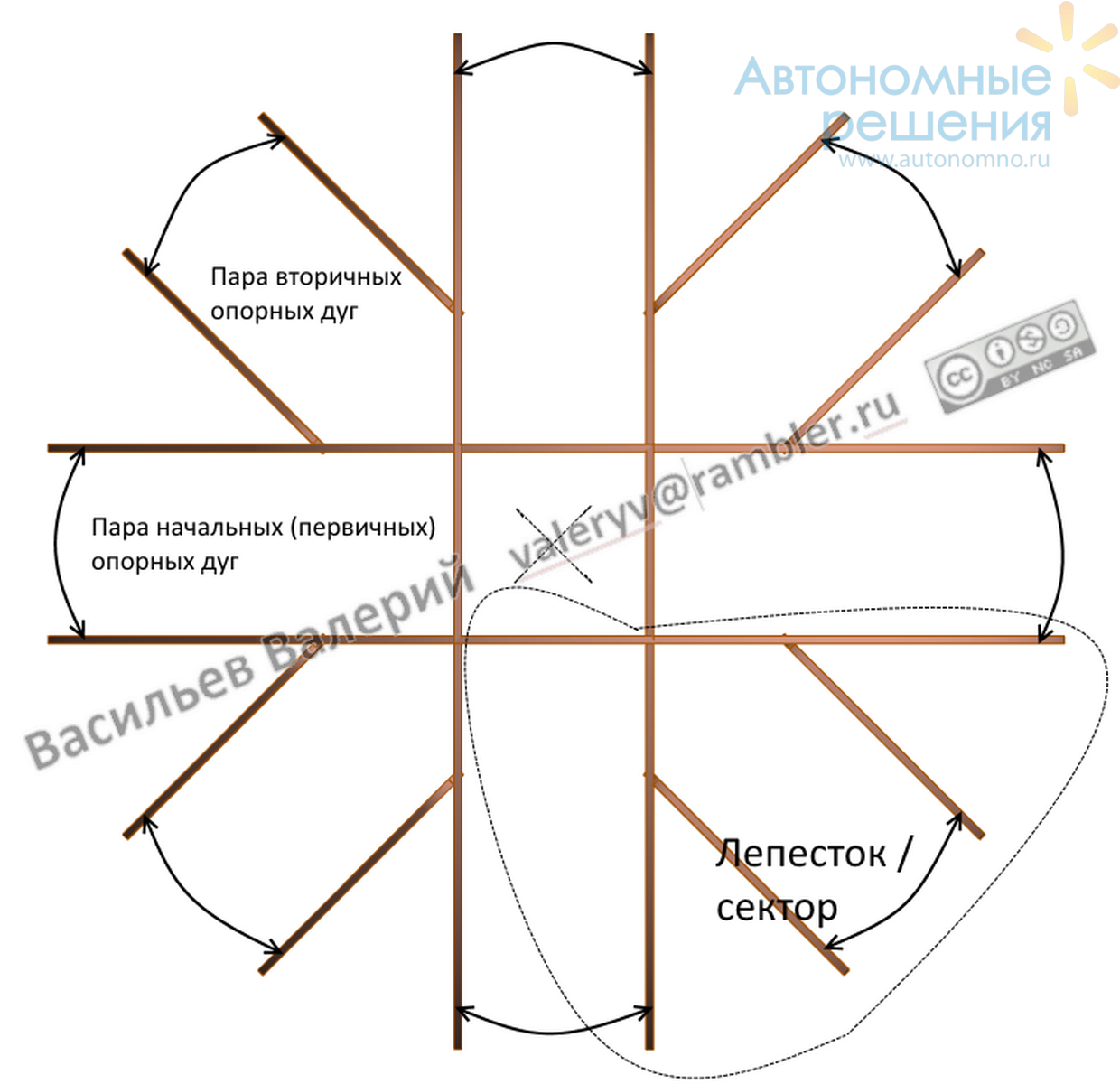
Рис.5 Восемь пар опорных дуг (пары показаны двойными стрелками), вид сверху
На рис.5 хорошо видно, что конструктив и покрытие в общем случае имеют симметрию вращения вокруг зенитной вертикали, а при числе лепестков кратно 4-м симметрия будет осевой.
Поворот копий начальных направляющих может быть произведён с шагом на угол = 1/n угла между направляющими из соседних пар, где в общем случае n-любое целое число ≥ 2.
В верхней части «само собою» образуется зенитное окно в виде многоугольника с числом сторон, равным числу лепестков в конструкции.
На рис.6 шаг поворота начальных направляющих составляет 1/3 угла между направляющими из соседних пар, то есть 30°, в основании 24-х угольник.

Рис.6 Двенадцать пар опорных дуг
При повороте начальных направляющих на 1/4 угла между направляющими из соседних пар, то есть 22,5°, в основании 4-х лепестковой конструкции 32-х угольник, рис.7.
Конечно, необязательно придерживаться правила: a=b. В некоторых случаях выгодно сделать а<b или a>b.
Понятно, что можно и дальше дробить лепестки, набирая нужный диаметр, но есть и другой путь – изменить количество лепестков.
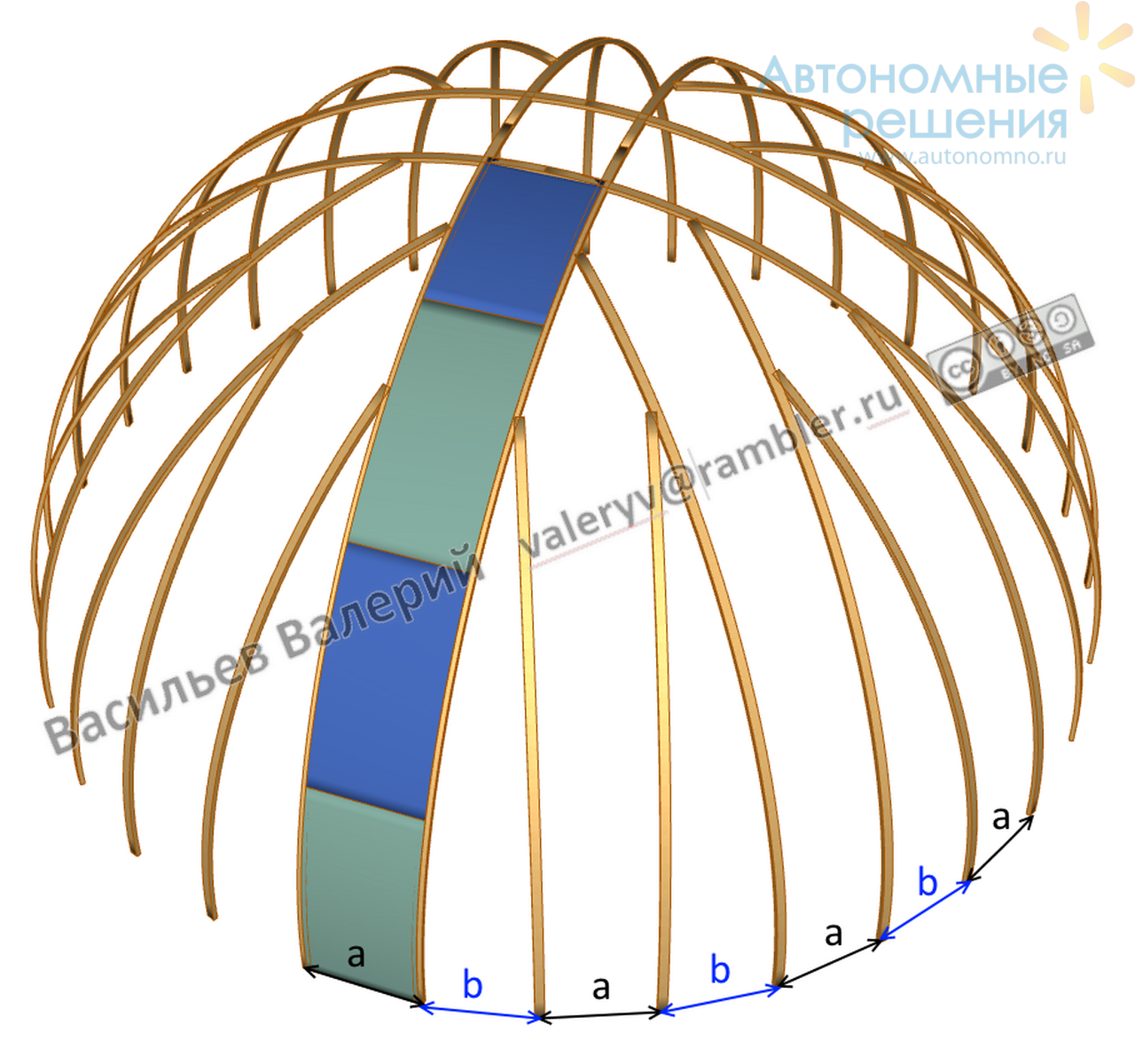
Рис.7 4-х лепестковая конструкция, 16 пар опорных дуг. Раскладка листов размера a*2a на одной начальной поверхности
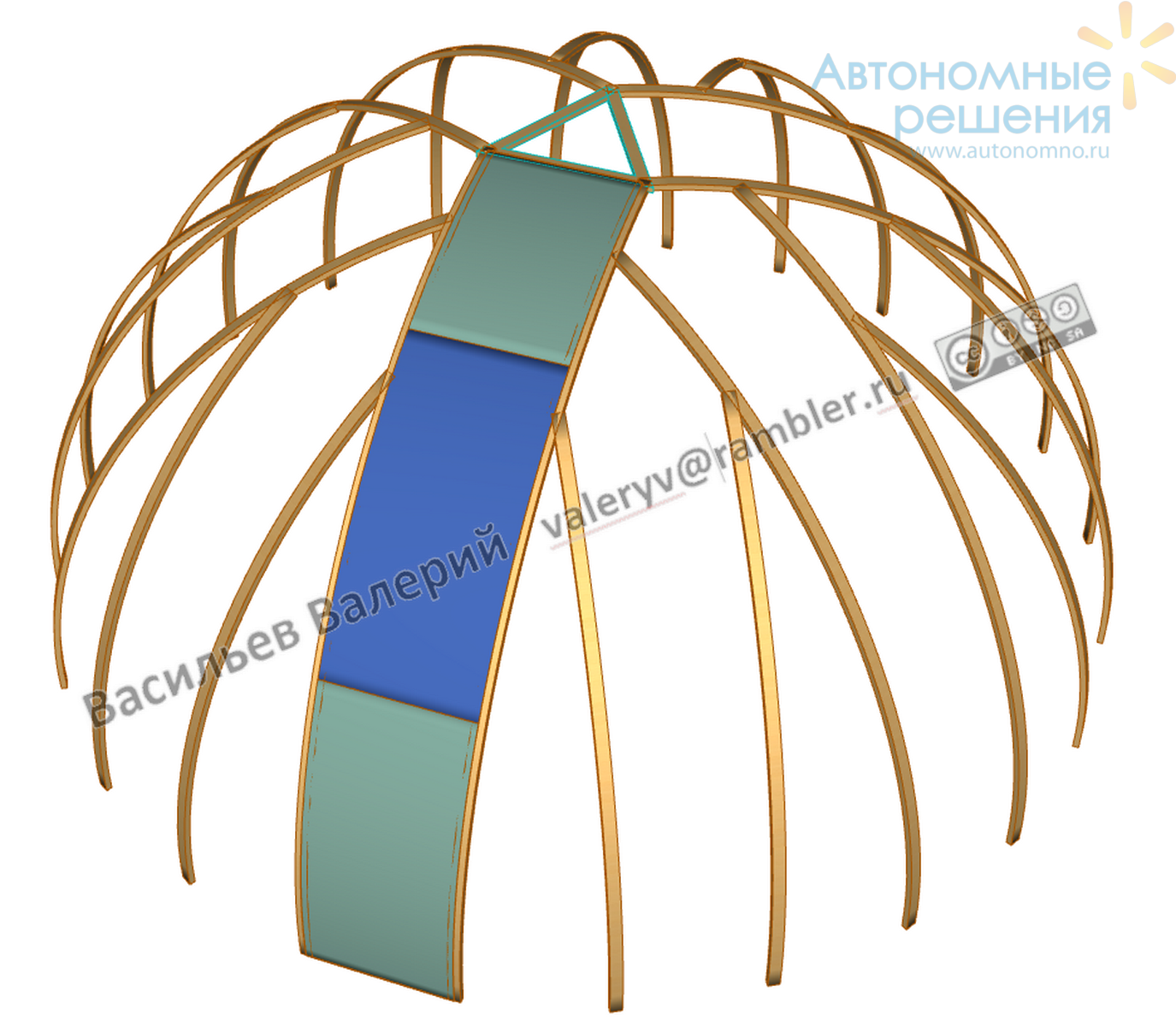
Рис.8 3-х лепестковкая конструкция, 12 пар опорных дуг
Раскладка листов размера a*2a на одной начальной поверхности

Рис.9 5-и лепестковая конструкция, 20 пар опорных дуг
Раскладка листов размера a*2a на первичной, вторичной и третичной поверхностях
На мой взгляд очень эстетичная и красивая пятилепестковая конструкция с 40-угольником в основании. При ширине листа а = 1250мм, радиус внешних поверхностей опорных дуг = 7966 мм
В выше приведённых примерах речь шла только о сферических конструкциях. Но такое разбиение возможно не только для сферы. Аналогичным образом можно укрыть любой эллипсоид вращения (вытянутый или сплюснутый сфероид), как показано, например, на рис.10.
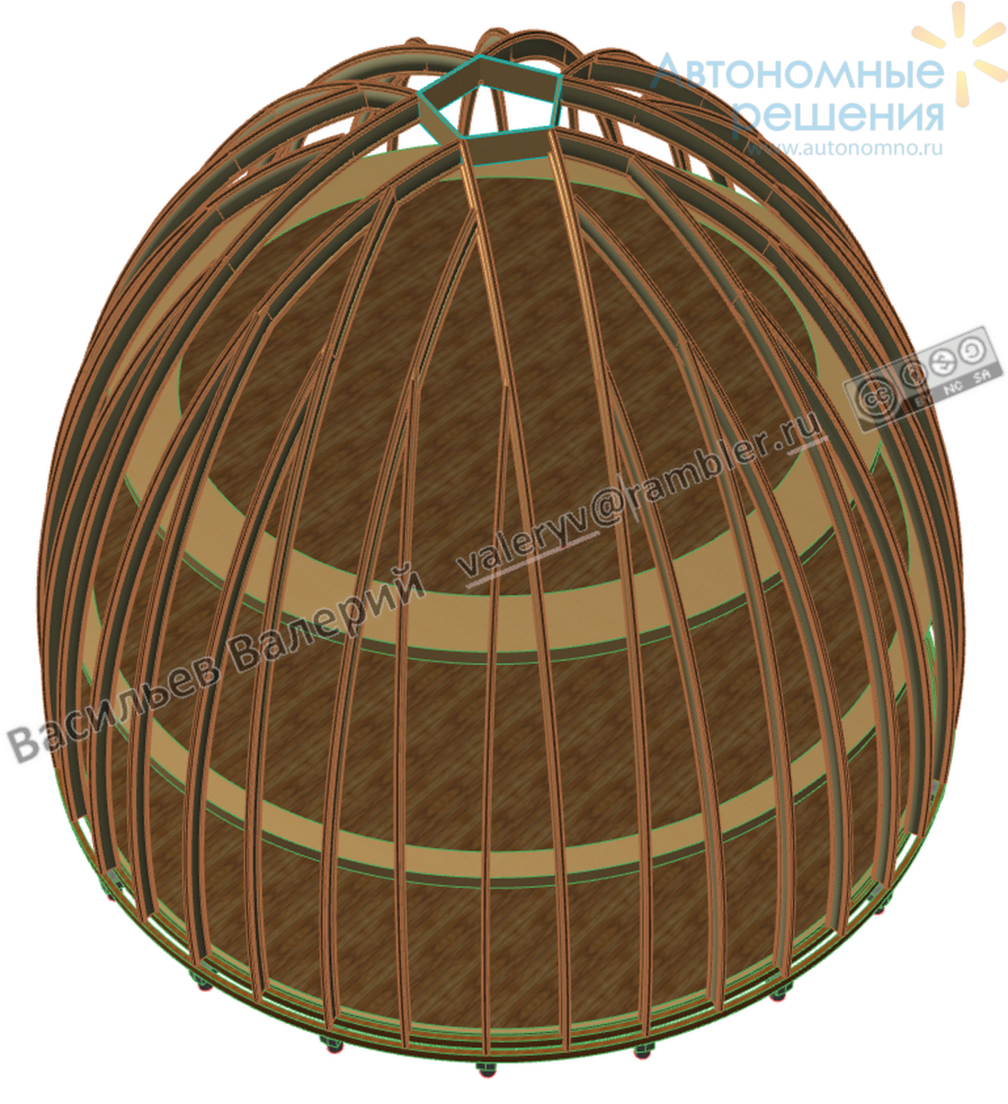
Рис.10 Вытянутый сфероидный купол, 5-и лепестковая конструкция, 20 пар опорных дуг
Вытянутый сфероидный купол, диаметр 15932 (а=1250), высота 11930 (верхние грани пятиугольника). Три уровня, высота потолков на 1-м и 2-м уровнях – 3500. Светлокоричневым и тёмнокоричневым наглядно показано соотношение площадей на разных уровнях «до 1700 мм» и «свыше 1700 мм» по вертикали от пола до внутренней оболочки.
Коэффициент заполнения полусфероидной поверхности прямоугольными листами согнутыми по цилиндрическим направляющим во различных вариантах около 60%. Остальные элементы – сферические трапеции и сферические равнобедренные треугольники (форма немного искажена, при раскрое боковые грани этих фигур не являются прямыми).
Показанные конструкции лишены излишней частотности в зените, присущей стратодезическим куполам и позволяют монтировать окна шириной чуть менее горизонтального размера листов на любом уровне без вырезания частей опорных дуг.
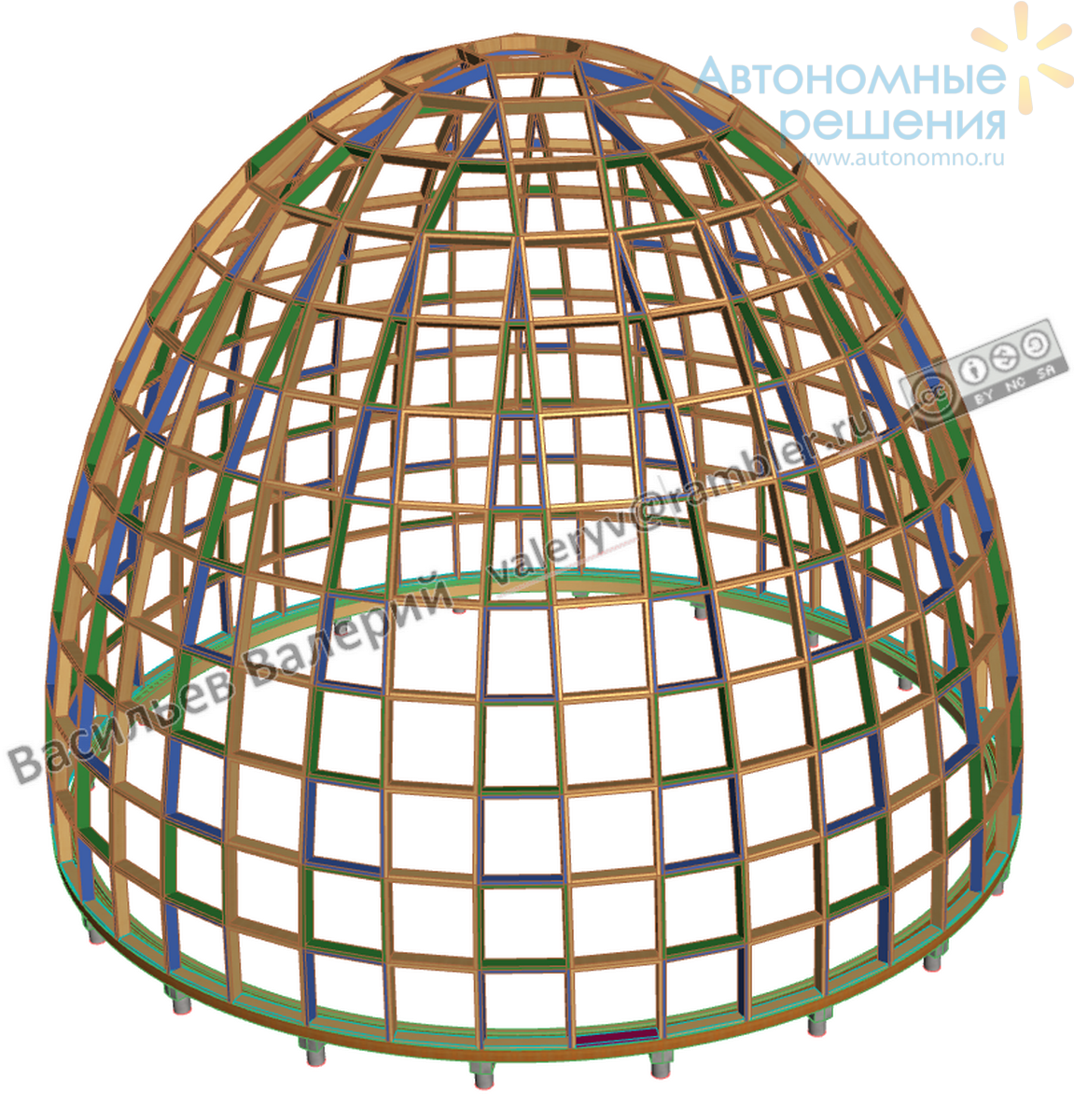
Рис.11а Ячеечный (рамочно-панельный) вытянутый сфероидный купол, 5 лепестков
Рамки для панелей приведены на рис.11б, 11в.

Рис.11б Рамки для трапецеидальных (зелёная) и квадратных (древесного цвета) панелей

Рис.11в Варианты исполнения квадратной рамки с удвоенными полками
Если выполнять рамки, как показано на рис. 11в, то трапецеидальные и треугольные рамки не требуются. Все рамки имеют однотипную квадратную или прямоугольную форму (края квадратного листа показаны штриховым линиями). Горизонтальные планки могут быть различной ширины и толщины.
Для сферы все рамки можно сделать одинаковыми, рис.11г (иногда удобнее использовать два типоразмера). В эллипсоидальных конструкциях боковые рёбра рамок будут отличаться углами подреза, хотя и здесь можно привести все рамки к единым углам, используя для стыковки рамок клинообразные вставки нужных углов.
Листы трапецеидальной и треугольной форм своими вертикальными сторонами накладываются встык с квадратными листами, закрывая добавочные вертикальные планки (тёмнокоричневые), а их горизонтальные стороны стыкуются по горизонтальным планкам. Горизонтальные планки монтируются по месту в процессе сборки, при этом ими удобно нивелировать погрешности исполнения рамок.
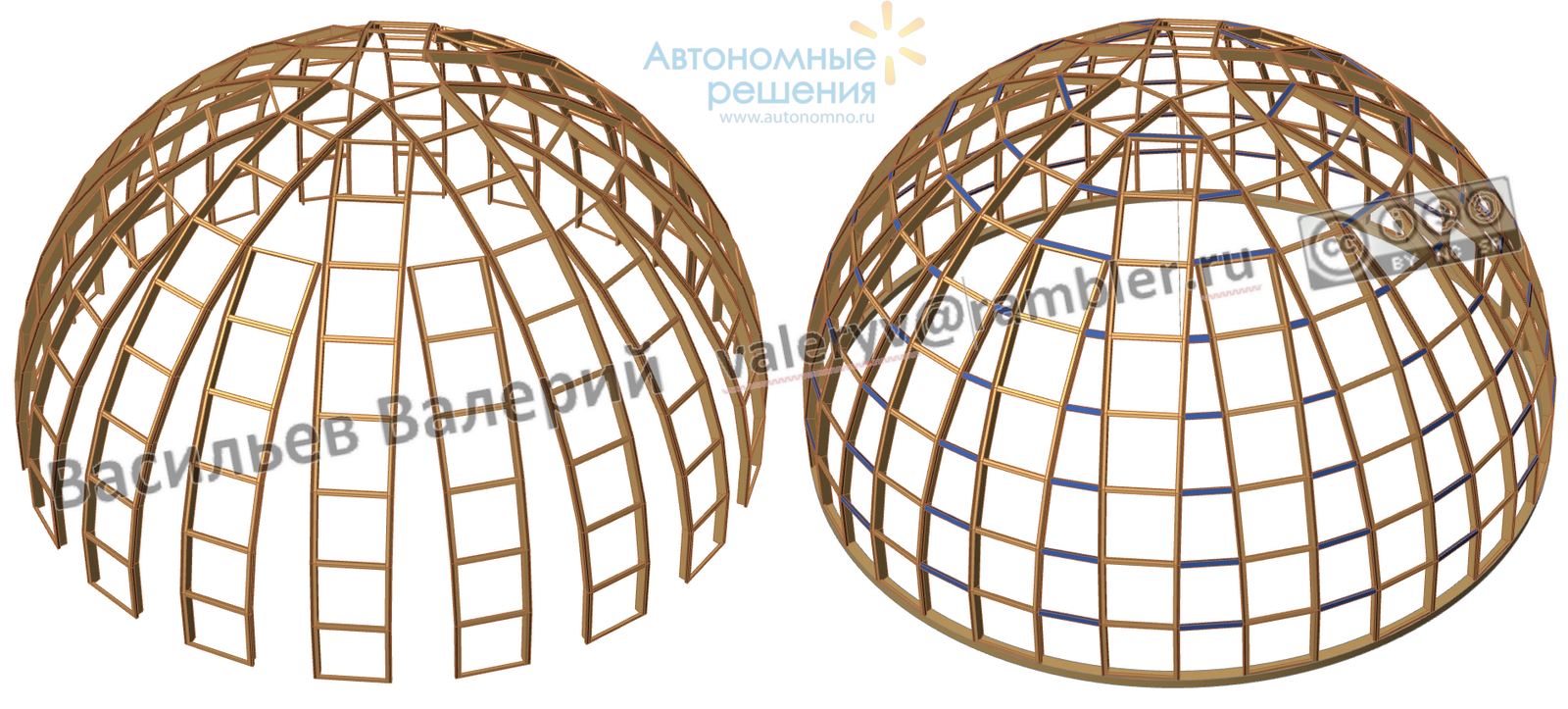
Рис.11г Ячеечный вытянутый сферический купол, 5 лепестков, 145 одинаковых квадратных ячеек с дополнительными линейными связующими (показаны синим цветом).
При а=1250, диаметр купола ~15650мм, максимальная высота конструктива 7543 мм
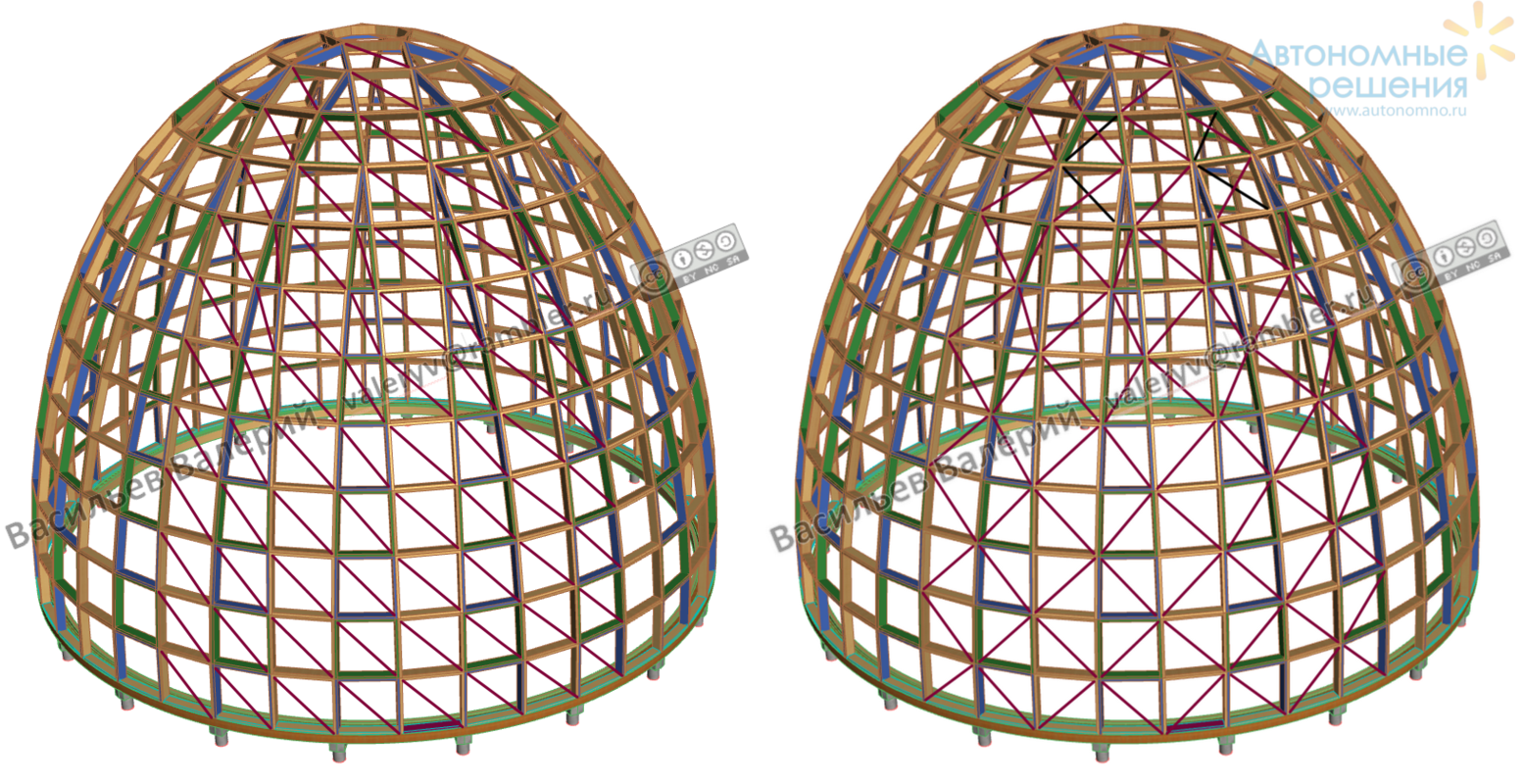
Рис.11д Ячеечный купол с дополнительными связями (укосами – показаны только на одном лепестке)
Конструкция на рис.11а и 11д выполнена как трапецеидальный купол, в котором каждая ячейка это плоская квадратная или в общем случае прямоугольная панель на основе рамки. В приведённом варианте половина всех панелей – квадраты. В случае конструкций, приведённых на рис.11д укосы делают структуру похожей на купола Шведлера.
Цилиндрическую поверхность можно образовывать более чем двумя параллельными опорными дугами. Это позволяет увеличить коэффициент заполнения полусфероидной поверхности прямоугольными листами. Пример такого разбиения приведён на рис.11е
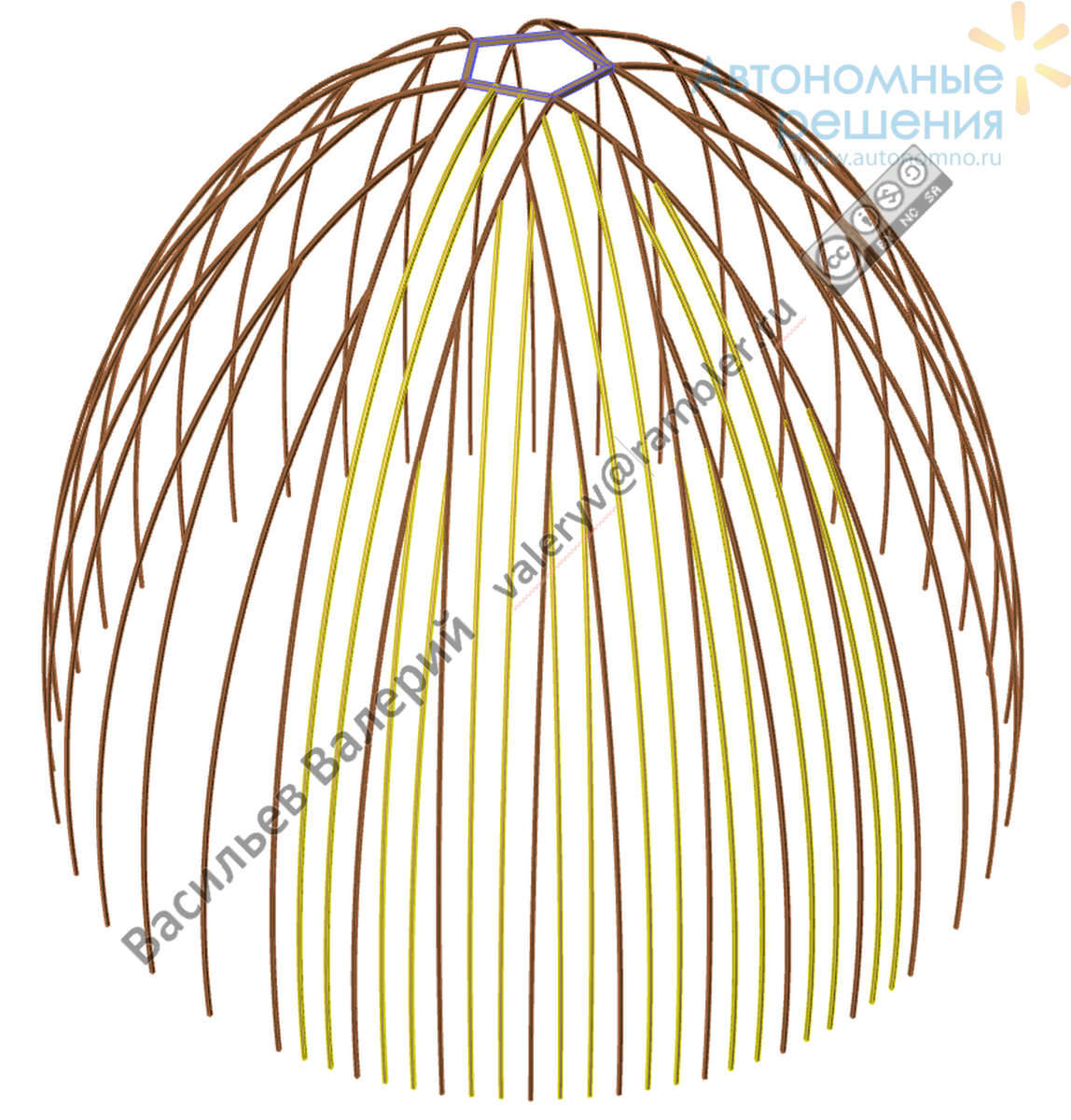
Рис.11е Вариант образования цилиндрических поверхностей 4-мя параллельными опорными дугами
Вариант довольно близкий к приведённому мною был предложен CiuDum на странице http://forum.domesworld.ru/viewtopic.php?f=31&p=11509#p11509, рис.12
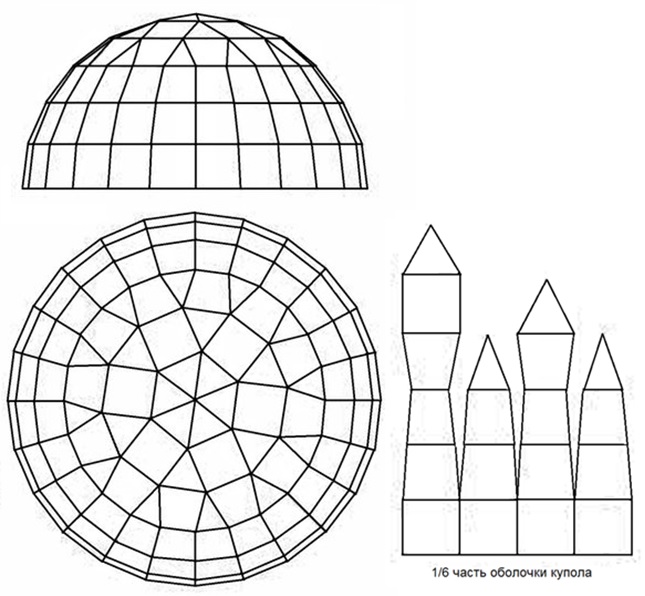
Рис.12 «… вариант покрытия купола из квадратных и почти квадратных панелей
(и несколько треугольников).»
Очень интересный и красивый вариант, но в нижнем ярусе только половина секций будет прямоугольниками, другая половина – трапеции, коэффициент покрытия прямоугольниками невелик.
Вот так может выглядеть дощатая обшивка пятилепесткового купола изнутри (рис.13а, рис.13б и снаружи рис.13в):

Рис. 13а Дощатая обшивка пятилепесткового купола, вид изнутри в зенит

Рис. 13б Дощатая обшивка пятилепесткового купола, вид изнутри на верхнюю боковую часть

Рис. 13в Дощатая внутренняя обшивка пятилепесткового купола вид снаружи без внешней оболочки
На сайте http://www.steeldome.ru GEK (участник форума http://forum.domesworld.ru) показал, что купол может быть выполнен из металлического листа. В показанном мною способе образования сферических поверхностей также возможно использовать металлические листы и даже полосы. Можно соединять листы или полосы:
- через полоски по стыкам листов (рис.14); внахлёст, по дугам (деревянным, металлическим и др.);
- при помощи металлических тавров (на рис.15 - рёбра тавров смотрят наружу); при помощи фальцевых соединений.
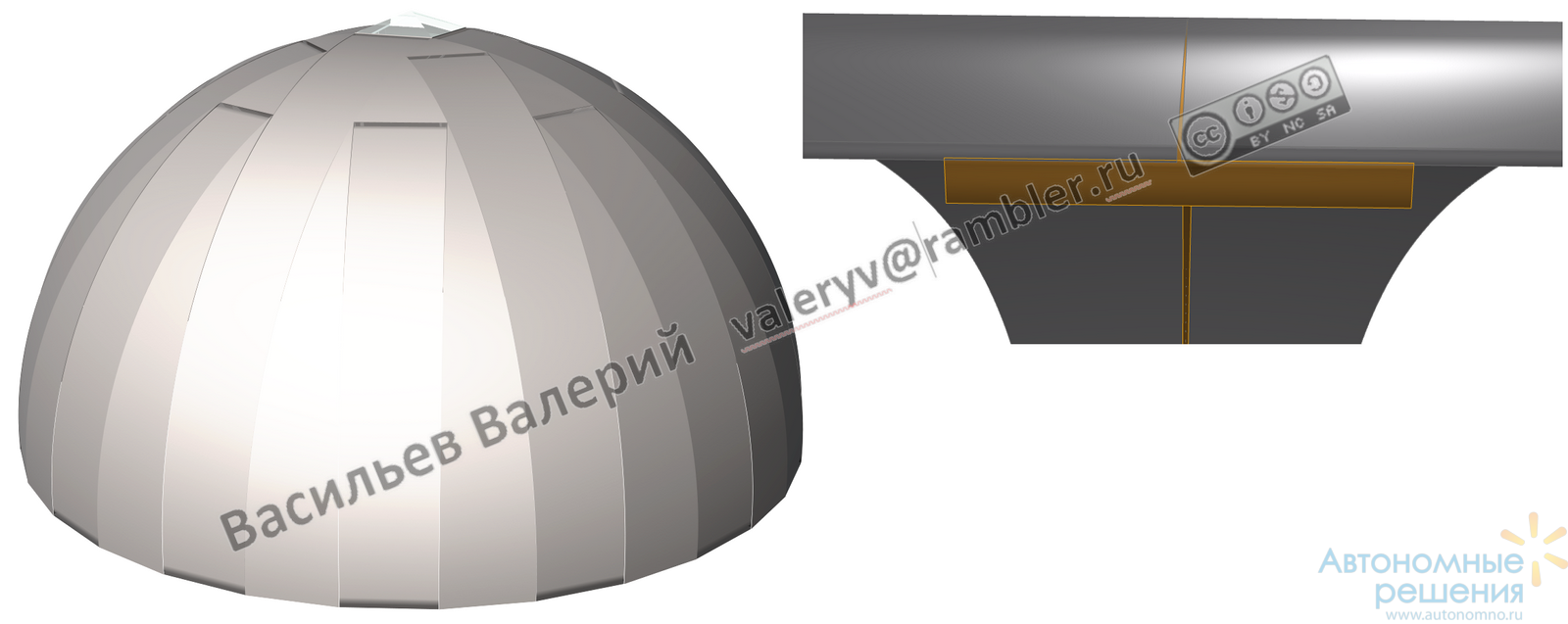
Рис.14 Купол из металлических листов и соединение листов через полоски по стыкам (полоски показаны золотистым цветом)

Рис.15 Купол из металлических листов и соединение листов при помощи тавров (тавры показаны золотистым цветом)
Требуется только резка металла, сверление отверстий и в некоторых случаях гибка. Сварка не требуется, а это довольно дорогая операция особенно по нержавеющей стали.
На рисунках 16-21 приведены конструкции каркасов на основе парных параллельных опорных дуг для различных форм купольных и не только купольных домов.

Рис.16 Каркас дома-яйца на основе вытянутого сфероида (>1/2 сфероида), в нижней части отрицательный уклон
Конструкция, приведённая на рис.16, объединяет пространственные преимущества башни и купола.

Рис. 17 Вытянутый сфероидный купол (слева) и производные от него (сфероид может быть и сплюснутый и шарообразный)

Рис. 18 Слева купол – половина трёхосного эллипсоида с осями различной длины, спереди - «диск» на основе эллипсоида, справа – ещё одна производная от вытянутого сфероида

Рис. 19 ПолуТор – завораживающая многоножка, на основе эллипсоидальных дуг

Рис. 20 ПолуТор, развёрнутый в "гусеницу"
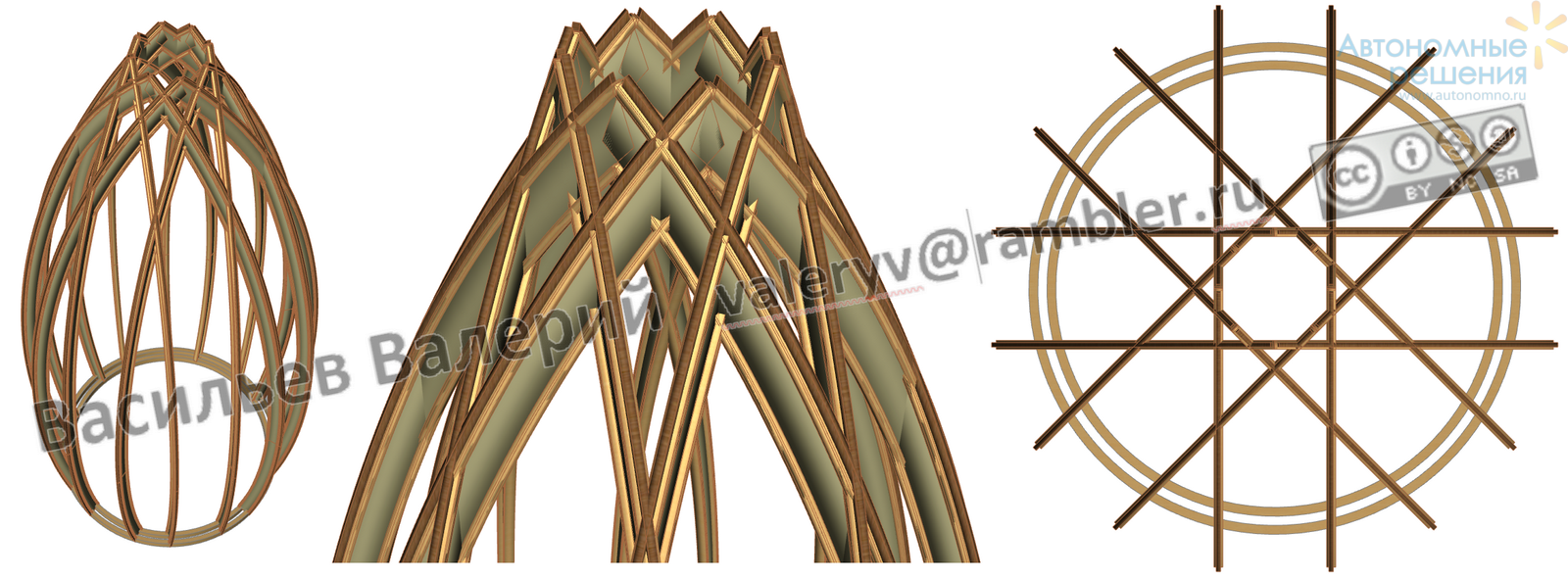
Рис. 21 Конструкция «Тюльпан», 3D виды и вид сверху
Конструкция, приведённая на рис.21, ещё один вариант "сотрудничества" башни и купола. Здесь снегу уже очень тяжело за что-то зацепиться.
